'로짓 회귀분석 Logistic Regression'으로 김밥 선호도 예측해보기
김밥, 데이터 사이언스의 재료가 되다
김밥은 대한민국 국민이라면 누구나 익숙한 음식입니다. 간편하고 다양한 재료로 만들어지며, 남녀노소 가리지 않고 사랑받는 대표적인 간식 또는 한 끼 식사죠. 그런데 이 ‘김밥’을 데이터로 분석해볼 수 있을까요?
이번 포스팅에서는 로짓 회귀분석(Logistic Regression) 기법을 활용해 김밥 선호도를 예측해보는 과정을 살펴보겠습니다. 이 과정을 통해 기초 통계학과 데이터 사이언스에 대한 이해를 높일 수 있을 뿐만 아니라, 실생활 데이터를 분석하는 흥미로운 사례도 접할 수 있습니다.

로짓 회귀분석이란 무엇인가?
로짓 회귀분석(Logistic Regression)은 종속 변수가 범주형(binary classification)인 경우에 사용하는 통계적 모델입니다. 즉, 결과가 ‘좋다/나쁘다’, ‘선호/비선호’, ‘성공/실패’처럼 두 가지 중 하나일 때 적합한 분석 기법입니다.
로짓 회귀의 핵심 아이디어는 선형 회귀의 결과를 로짓 함수(logit function)로 변환해 확률로 해석 가능하게 만든다는 점입니다. 수식은 다음과 같습니다:
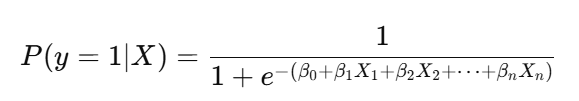
이때 $P(y=1|X)$는 김밥을 '선호한다'는 확률이고, $X_1, X_2, ..., X_n$은 개인의 특성이나 김밥의 재료, 상황 등을 설명하는 독립 변수입니다.
데이터 설계: 김밥 선호도 예측을 위한 가상의 데이터
김밥 선호도를 예측하기 위해 아래와 같은 변수들을 설정해 봅니다.
| 변수명 | 설명 | 타입 |
|---|---|---|
| age | 나이 | 연속형 |
| gender | 성별 (0: 여성, 1: 남성) | 이진형 |
| rice_type | 밥 종류 (0: 흰쌀밥, 1: 현미밥) | 이진형 |
| filling | 속재료 (0: 단무지 중심, 1: 불고기 중심) | 이진형 |
| spicy_sauce | 매운 소스 사용 여부 (0: 미사용, 1: 사용) | 이진형 |
| prefer_kimbap | 김밥 선호 여부 (0: 비선호, 1: 선호) | 이진형 (종속변수) |
우리는 위 데이터를 기반으로 사람들이 김밥을 선호하는 확률을 추정하고, 어떤 요인이 선호도에 영향을 미치는지 분석하고자 합니다.
로짓 회귀분석 모델 학습 과정
데이터 전처리
- 결측값 처리, 범주형 변수의 숫자화
- 데이터 정규화 필요 여부 확인
모델 구축
로짓 회귀모델을 사용하여 다음과 같은 회귀식을 학습합니다.
\text{logit}(P) = \beta_0 + \beta_1 \cdot \text{age} + \beta_2 \cdot \text{gender} + \beta_3 \cdot \text{rice_type} + \beta_4 \cdot \text{filling} + \beta_5 \cdot \text{spicy_sauce}모델 해석
각 계수(β)의 부호와 크기를 통해, 어떤 요인이 김밥 선호도에 유의미한 영향을 주는지를 파악합니다. 예를 들어:- $\beta_4$가 양수이고 유의하다면, ‘불고기 중심 김밥’이 선호도를 높인다는 해석이 가능합니다.
- $\beta_5$가 음수이면, ‘매운 소스’가 선호도를 떨어뜨릴 수 있다는 뜻입니다.
모델 평가 지표
- 정확도 (Accuracy)
- 정밀도와 재현율 (Precision, Recall)
- ROC-AUC 커브
Python 코드 예시 (간략 구현)
import pandas as pd
import statsmodels.api as sm
# 가상의 데이터 생성
data = pd.DataFrame({
'age': [25, 34, 29, 42, 19, 60, 35, 27],
'gender': [0, 1, 1, 0, 0, 1, 1, 0],
'rice_type': [0, 1, 0, 1, 0, 1, 1, 0],
'filling': [1, 1, 0, 1, 0, 0, 1, 1],
'spicy_sauce': [0, 1, 1, 0, 0, 1, 1, 0],
'prefer_kimbap': [1, 1, 0, 1, 0, 0, 1, 1]
})
# 독립변수와 종속변수 분리
X = data[['age', 'gender', 'rice_type', 'filling', 'spicy_sauce']]
X = sm.add_constant(X) # 절편항 추가
y = data['prefer_kimbap']
# 로짓 모델 적합
model = sm.Logit(y, X)
result = model.fit()
# 결과 출력
print(result.summary())해석: 결과를 어떻게 이해할까?
분석 결과에서 각 변수의 P-value가 0.05 미만이라면, 그 변수는 통계적으로 유의미하다고 볼 수 있습니다. 예를 들어:
filling변수의 계수가 양수이고 p-value가 0.01일 경우 → 불고기 중심 김밥이 선호도 증가와 관련 있음age의 계수가 음수일 경우 → 나이가 많을수록 김밥 선호도가 떨어짐을 의미할 수 있음
실생활 활용 사례
- 프랜차이즈 김밥 매장 전략 수립
특정 연령대나 성별, 취향에 맞춰 김밥 메뉴를 기획할 수 있습니다. 예: 청년층에는 매운 불고기 김밥, 노년층에는 저자극 클래식 김밥 - 온라인 주문 플랫폼의 추천 알고리즘 개선
유저 정보(나이, 성별 등)를 바탕으로 맞춤형 김밥 메뉴를 추천할 수 있습니다. - 오프라인 매장 재고 전략
특정 시간대, 고객층에 따라 선호도 높은 메뉴를 중심으로 재료를 준비해 재고 효율화 가능
한계 및 주의사항
- 로짓 회귀는 선형 경계를 기반으로 작동하므로, 변수 간의 비선형 관계가 있는 경우 성능이 제한적일 수 있습니다.
- 과적합을 방지하기 위해 정규화 기법(L1, L2)이나 교차검증이 필요할 수 있습니다.
- 실제 데이터에서는 표본 크기와 대표성 확보가 중요합니다.
결론: 로짓 회귀로 ‘김밥 취향’까지 파악한다?
로짓 회귀분석은 단순한 수학 모델이 아니라, 사람들의 선택 이면에 있는 논리를 예측하는 도구입니다. 김밥이라는 일상적인 주제를 통해 이를 접근해보면, 데이터 분석이 얼마나 실생활에 밀접하고 흥미로운 분야인지를 실감할 수 있습니다. 나아가, 더 복잡한 머신러닝 기법으로 확장하는 기초적인 이해를 도울 수 있는 중요한 관문이기도 합니다.

'마케팅관련' 카테고리의 다른 글
| 다차원척도법으로 브랜드 감성 시각화 실험 (0) | 2025.05.10 |
|---|---|
| 시간적 자기상관(Autocorrelation)을 무시한 캠페인 예산 편성의 실패 사례 (0) | 2025.05.09 |
| 지각도지도(Perceptual Map)에서 등장하지 않는 브랜드의 마케팅 전략 (0) | 2025.05.08 |
| 베이지안 A/B 테스트가 소규모 이벤트에 부적합한 이유 (0) | 2025.05.07 |
| '군집분석'으로 자취생 유형 나눠본 결과 (1) | 2025.05.06 |




댓글